Discussion 9: Linked Lists, Efficiency, Mutable Trees

This is an online worksheet that you can work on during discussions. Your work is not graded and you do not need to submit anything.

Linked Lists

There are many different implementations of sequences in Python. Today, we'll explore the linked list implementation.

A linked list is either an empty linked list, or a Link object containing a first value and the rest of the linked list.

To check if a linked list is an empty linked list, compare it against the class attribute Link.empty:

if link is Link.empty:
    print('This linked list is empty!')
else:
    print('This linked list is not empty!')

You can find an implementation of the Link class below:

class Link:
    """A linked list."""
    empty = ()

    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest

    def __repr__(self):
        if self.rest:
            rest_repr = ', ' + repr(self.rest)
        else:
            rest_repr = ''
        return 'Link(' + repr(self.first) + rest_repr + ')'

    def __str__(self):
        string = '<'
        while self.rest is not Link.empty:
            string += str(self.first) + ' '
            self = self.rest
        return string + str(self.first) + '>'

Q1: WWPD: Linked Lists

What would Python display?

Note: If you get stuck, try drawing out the box-and-pointer diagram for the linked list or running examples in 61A Code.

>>> link = Link(1, Link(2, Link(3)))
>>> link.first
1 
>>> link.rest.first
2 
>>> link.rest.rest.rest is Link.empty
True 
>>> link.rest = link.rest.rest
>>> link.rest.first
3 
>>> link = Link(1)
>>> link.rest = link
>>> link.rest.rest.rest.rest.first
1 
>>> link = Link(2, Link(3, Link(4)))
>>> link2 = Link(1, link)
>>> link2.first
1 
>>> link2.rest.first
2 
>>> link = Link(1000, 2000)
Error (second argument of Link constructor must be a Link instance)
>>> link = Link(1000, Link())
Error (first argument of Link constructor must be specified)
>>> link = Link(Link("Hello"), Link(2))
>>> link.first
Link('Hello') 
>>> link = Link(Link("Hello"), Link(2))
>>> link.first.rest is Link.Empty
True 
>>> link = Link(Link("Hello"), Link(2))
>>> link.rest is Link.Empty
False

Write a function convert_link that takes in a linked list and returns the sequence as a Python list. You may assume that the input list is shallow; that is none of the elements is another linked list.

Try to find both an iterative and recursive solution for this problem!

Challenge: You may NOT assume that the input list is shallow, and we still want to return a flattened Python list as our output. Challenge Hint: Use the type built-in.

Your Answer Run in 61A Code
Solution 
def convert_link(link):
    """Takes a linked list and returns a Python list with the same elements.

    >>> link = Link(1, Link(2, Link(3, Link(4))))
    >>> convert_link(link)
    [1, 2, 3, 4]
    >>> convert_link(Link.empty)
    []
    """
    # Recursive solution
    if link is Link.empty:
        return []
    return [link.first] + convert_link(link.rest)

# Iterative solution
def convert_link_iterative(link):
    result = []
    while link is not Link.empty:
        result.append(link.first)
        link = link.rest
    return result

# Challenge solution
def convert_link_challenge(link):
    if link is Link.empty:
        return []
    if type(link.first) == Link:
        return [convert_link_challenge(link.first)] + convert_link_challenge(link.rest)
    return [link.first] + convert_link_challenge(link.rest)

Write a function duplicate_link that takes in a linked list link and a value. duplicate_link will mutate link such that if there is a linked list node that has a first equal to value, that node will be duplicated. Note that you should be mutating the original link list link; you will need to create new Links, but you should not be returning a new linked list.

Note: In order to insert a link into a linked list, you need to modify the .rest of certain links. We encourage you to draw out a doctest to visualize!

Your Answer Run in 61A Code
Solution 
def duplicate_link(link, val):
    """Mutates `link` such that if there is a linked list
    node that has a first equal to value, that node will
    be duplicated. Note that you should be mutating the
    original link list.

    >>> x = Link(5, Link(4, Link(3)))
    >>> duplicate_link(x, 5)
    >>> x
    Link(5, Link(5, Link(4, Link(3))))
    >>> y = Link(2, Link(4, Link(6, Link(8))))
    >>> duplicate_link(y, 10)
    >>> y
    Link(2, Link(4, Link(6, Link(8))))
    >>> z = Link(1, Link(2, (Link(2, Link(3)))))
    >>> duplicate_link(z, 2) #ensures that back to back links with val are both duplicated
    >>> z
    Link(1, Link(2, Link(2, Link(2, Link(2, Link(3))))))
    """
    if link is Link.empty:
        return
    elif link.first == val:
        remaining = link.rest
        link.rest = Link(val, remaining)
        duplicate_link(remaining, val)
    else:
        duplicate_link(link.rest, val)

Write a function that takes in a Python list of linked lists and multiplies them element-wise. It should return a new linked list.

If not all of the Link objects are of equal length, return a linked list whose length is that of the shortest linked list given. You may assume the Link objects are shallow linked lists, and that lst_of_lnks contains at least one linked list.

Your Answer
Run in 61A Code
Solution 
def multiply_lnks(lst_of_lnks):
    """
    >>> a = Link(2, Link(3, Link(5)))
    >>> b = Link(6, Link(4, Link(2)))
    >>> c = Link(4, Link(1, Link(0, Link(2))))
    >>> p = multiply_lnks([a, b, c])
    >>> p.first
    48
    >>> p.rest.first
    12
    >>> p.rest.rest.rest is Link.empty
    True
    """
    # Implementation Note: you might not need all lines in this skeleton code
    product = 1
    for lnk in lst_of_lnks:
        if lnk is Link.empty:
            return Link.empty
        product *= lnk.first
    lst_of_lnks_rests = [lnk.rest for lnk in lst_of_lnks]
    return Link(product, multiply_lnks(lst_of_lnks_rests))
For our base case, if we detect that any of the lists in the list of Links is empty, we can return the empty linked list as we're not going to multiply anything.

Otherwise, we compute the product of all the firsts in our list of Links. Then, the subproblem we use here is the rest of all the linked lists in our list of Links. Remember that the result of calling multiply_lnks will be a linked list! We'll use the product we've built so far as the first item in the returned Link, and then the result of the recursive call as the rest of that Link.

Next, we have the iterative solution:

def multiply_lnks(lst_of_lnks):
    """
    >>> a = Link(2, Link(3, Link(5)))
    >>> b = Link(6, Link(4, Link(2)))
    >>> c = Link(4, Link(1, Link(0, Link(2))))
    >>> p = multiply_lnks([a, b, c])
    >>> p.first
    48
    >>> p.rest.first
    12
    >>> p.rest.rest.rest is Link.empty
    True
    """
    # Alternate iterative approach
    import operator
    from functools import reduce
    def prod(factors):
         return reduce(operator.mul, factors, 1)

    head = Link.empty
    tail = head
    while Link.empty not in lst_of_lnks:
        all_prod = prod([l.first for l in lst_of_lnks])
        if head is Link.empty:
            head = Link(all_prod)
            tail = head
        else:
            tail.rest = Link(all_prod)
            tail = tail.rest
        lst_of_lnks = [l.rest for l in lst_of_lnks]
    return head

The iterative solution is a bit more involved than the recursive solution. Instead of building the list backwards as in the recursive solution (because of the order that the recursive calls result in, the last item in our list will be finished first), we'll build the resulting linked list as we go along.

We usehead and tail to track the front and end of the new linked list we're creating. Our stopping condition for the loop is if any of the Links in our list of Links runs out of items.

Finally, there's some special handling for the first item. We need to update both head and tail in that case. Otherwise, we just append to the end of our list using tail, and update tail.

Q5: Flip Two

Write a recursive function flip_two that takes as input a linked list s and mutates s so that every pair is flipped.

Your Answer
Run in 61A Code
Solution 
def flip_two(s):
    """
    >>> one_lnk = Link(1)
    >>> flip_two(one_lnk)
    >>> one_lnk
    Link(1)
    >>> lnk = Link(1, Link(2, Link(3, Link(4, Link(5)))))
    >>> flip_two(lnk)
    >>> lnk
    Link(2, Link(1, Link(4, Link(3, Link(5)))))
    """
    # Recursive solution:
    if s is Link.empty or s.rest is Link.empty:
        return
    s.first, s.rest.first = s.rest.first, s.first
    flip_two(s.rest.rest)

    # For an extra challenge, try writing out an iterative approach as well below!
    return # separating recursive and iterative implementations

    # Iterative approach
    while s is not Link.empty and s.rest is not Link.empty:
        s.first, s.rest.first = s.rest.first, s.first
        s = s.rest.rest
If there's only a single item (or no item) to flip, then we're done.

Otherwise, we swap the contents of the first and second items in the list. Since we've handled the first two items, we then need to recurse on s.rest.rest.

Although the question explicitly asks for a recursive solution, there is also a fairly similar iterative solution (see python solution).

We will advance s until we see there are no more items or there is only one more Link object to process. Processing each Link involves swapping the contents of the first and second items in the list (same as the recursive solution).

Efficiency

When we talk about the efficiency of a function, we are often interested in the following: as the size of the input grows, how does the runtime of the function change? And what do we mean by runtime?

Example 1: square(1) requires one primitive operation: multiplication. square(100) also requires one. No matter what input n we pass into square, it always takes a constant number of operations (1). In other words, this function has a runtime complexity of Θ(1).

As an illustration, check out the table below:

input function call return value operations
1 square(1) 1*1 1
2 square(2) 2*2 1
... ... ... ...
100 square(100) 100*100 1
... ... ... ...
n square(n) n*n 1

Example 2: factorial(1) requires one multiplication, but factorial(100) requires 100 multiplications. As we increase the input size of n, the runtime (number of operations) increases linearly proportional to the input. In other words, this function has a runtime complexity of Θ(n).

As an illustration, check out the table below:

input function call return value operations
1 factorial(1) 1*1 1
2 factorial(2) 2*1*1 2
... ... ... ...
100 factorial(100) 100*99*...*1*1 100
... ... ... ...
n factorial(n) n*(n-1)*...*1*1 n

Example 3: Consider the following function:

def bar(n):
    for a in range(n):
        for b in range(n):
            print(a,b)

bar(1) requires 1 print statements, while bar(100) requires 100*100 = 10000 print statements (each time a increments, we have 100 print statements due to the inner for loop). Thus, the runtime increases quadratically proportional to the input. In other words, this function has a runtime complexity of Θ(n^2).

input function call operations (prints)
1 bar(1) 1
2 bar(2) 4
... ... ...
100 bar(100) 10000
... ... ...
n bar(n) n^2

Example 4: Consder the following function:

def rec(n):
    if n == 0:
        return 1
    else:
        return rec(n - 1) + rec(n - 1)

rec(1) requires one addition, as it returns rec(0) + rec(0), and rec(0) hits the base case and requires no further additions. but rec(4) requires 2^4 - 1 = 15 additions. To further understand the intuition, we can take a look at the recurisve tree below. To get rec(4), we need one addition. We have two calls to rec(3), which each require one addition, so this level needs two additions. Then we have four calls to rec(2), so this level requires four additions, and so on down the tree. In total, this adds up to 1 + 2 + 4 + 8 = 15 additions.

Recursive Call Tree

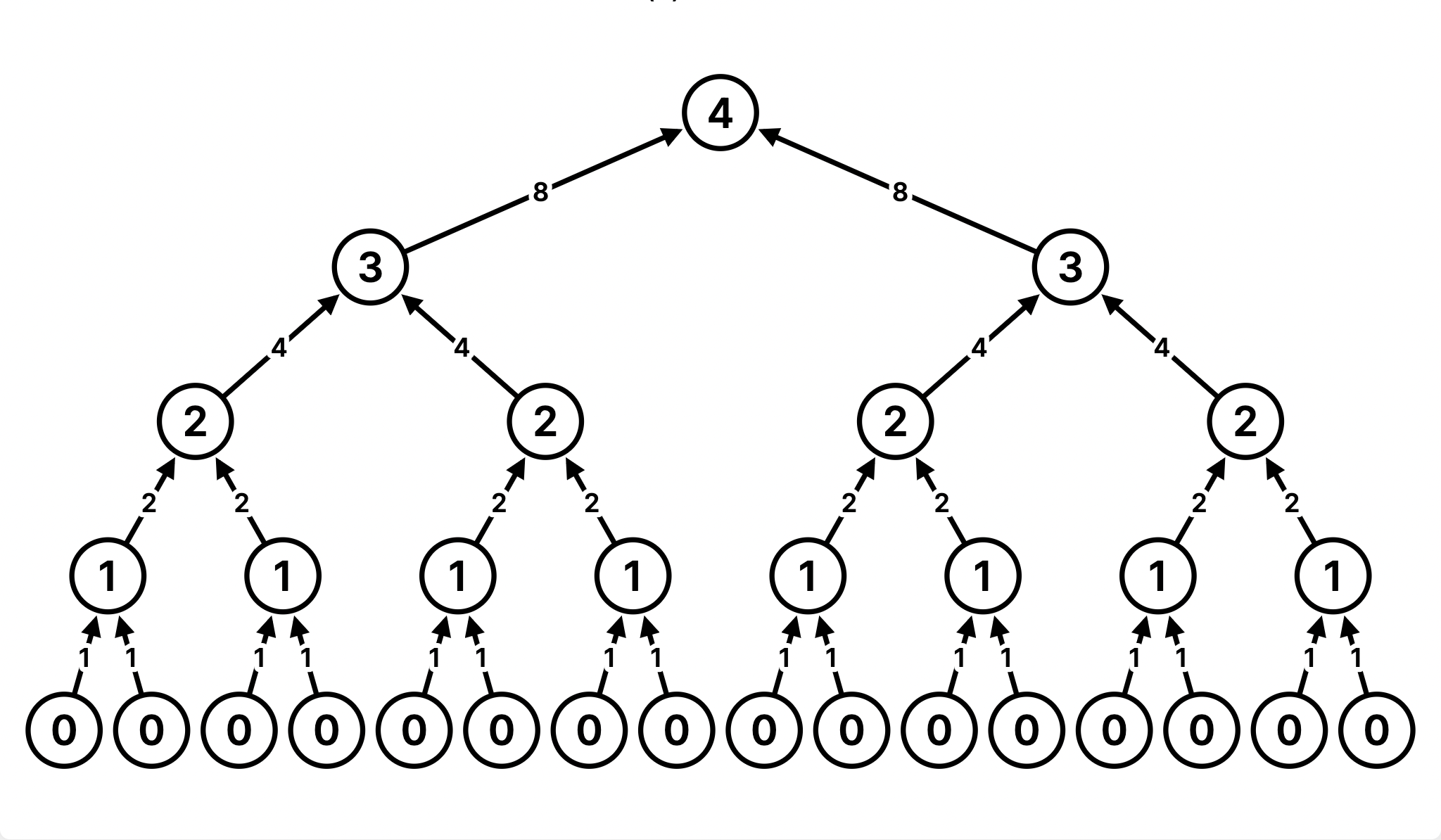
As we increase the input size of n, the runtime (number of operations) increases exponentially proportional to the input. In other words, this function has a runtime complexity of Θ(2^n).

As an illustration, check out the table below:

input function call return value operations
1 rec(1) 2 1
2 rec(2) 4 3
... ... ... ...
10 rec(10) 1024 1023
... ... ... ...
n rec(n) 2^n 2^n

Here are some general guidelines for finding the order of growth for the runtime of a function:

  • If the function is recursive or iterative, you can subdivide the problem as seen above:

    • Count the number of recursive calls/iterations that will be made in terms of input size n.
    • Find how much work is done per recursive call or iteration in terms of input size n.
    • The answer is usually the product of the above two, but be sure to pay attention to control flow!
  • If the function calls helper functions that are not constant-time, you need to take the runtime of the helper functions into consideration.
  • We can ignore constant factors. For example 1000000n and n steps are both linear.
  • We can also ignore smaller factors. For example if h calls f and g, and f is Quadratic while g is linear, then h is Quadratic.

  • For the purposes of this class, we take a fairly coarse view of efficiency. All the problems we cover in this course can be grouped as one of the following:

    • Constant: the amount of time does not change based on the input size. Rule: n --> 2n means t --> t.
    • Logarithmic: the amount of time changes based on the logarithm of the input size. Rule: n --> 2n means t --> t + k.
    • Linear: the amount of time changes with direct proportion to the size of the input. Rule: n --> 2n means t --> 2t.
    • Quadratic: the amount of time changes based on the square of the input size. Rule: n --> 2n means t --> 4t.
    • Exponential: the amount of time changes with a power of the input size. Rule: n --> n + 1 means t --> 2t.

Q6: The First Order...of Growth

What is the efficiency of rey?

def rey(finn):
    poe = 0
    while finn >= 2:
        poe += finn
        finn = finn / 2
    return

Choose one of:

  • Constant
  • Logarithmic
  • Linear
  • Quadratic
  • Exponential
  • None of these
Logarithmic, because our while loop iterates at most log(finn) times, due to finn being halved in every iteration. This is commonly known as Θ(log(finn)) runtime. Another way of looking at this if you duplicate the input, we only add a single iteration to the time, which also indicates logarithmic.

What is the efficiency of mod_7?

def mod_7(n):
    if n % 7 == 0:
        return 0
    else:
        return 1 + mod_7(n - 1)

Choose one of:

  • Constant
  • Logarithmic
  • Linear
  • Quadratic
  • Exponential
  • None of these
Constant, since in the worst case scenario our function mod_7 will require 6 recursive calls to reach the base case. Consider the worst case where we have an input n such that our first call to mod_7 evaluates n % 7 as 6. Each recursive call will decrement n by 1, allowing us to eventually reach the base case of returning 0 in 6 recursive calls (n will range from 0 to 6). Since the growth of the computation is independent of the input, we say this is constant, which is commonly known as a Θ(1) runtime.

Additional Practice: Trees

Q7: Find Paths

Hint: This question is similar to find_path on Discussion 05.

Define the procedure find_paths that, given a Tree t and an entry, returns a list of lists containing the nodes along each path from the root of t to entry. You may return the paths in any order.

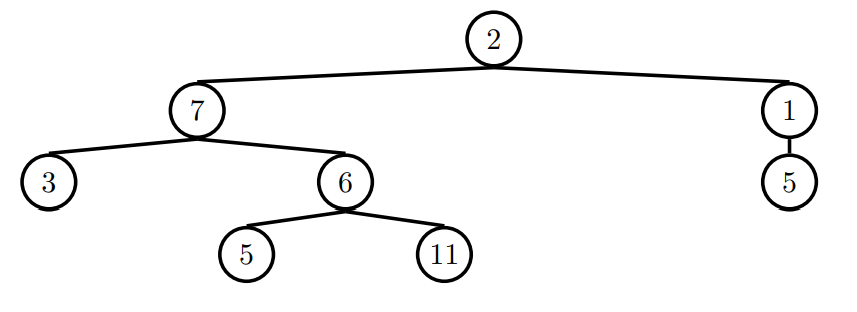
For instance, for the following tree tree_ex, find_paths should behave as specified in the function doctests. Example Tree

Your Answer
Run in 61A Code
Solution 
def find_paths(t, entry):
    """
    >>> tree_ex = Tree(2, [Tree(7, [Tree(3), Tree(6, [Tree(5), Tree(11)])]), Tree(1, [Tree(5)])])
    >>> find_paths(tree_ex, 5)
    [[2, 7, 6, 5], [2, 1, 5]]
    >>> find_paths(tree_ex, 12)
    []
    """

    paths = []
    if t.label == entry:
        paths.append([t.label])
    for b in t.branches:
        for path in find_paths(b, entry):
            paths.append([t.label] + path)
    return paths